學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中奪取佳績的學生。
·本周試題由學而思教研部《小學奧數系統總復習》編者白亞娟老師精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
【計數專題】
1.難度:★★
把一元錢換成角幣,有多少種換法?人民幣角幣的面值有五角、二角、一角三種.
【解析】把一元錢換成角幣,有三類分法:①第一類:有五角幣2張,只有1種換法:
②第二類:有五角幣1張,則此時二角幣可以有0,1,2張,相應的,一角幣有5,3,1張,有3種換法;
③第三類:有五角幣0張,則此時二角幣可以有0,1,2,3,4,5張,相應的,一角幣有10,8,6,4,2,0張,有6種換法.
所以,根據加法原理,總共的換法有1+3=6=10種.
2.難度:★★
如圖,某城市的街道由5條東西向馬路和7條南北向馬路組成,現在要從西南角的A處沿最短的路線走到東北角B出,由于修路,十字路口C不能通過,那么共有____種不同走法.
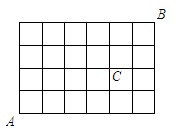
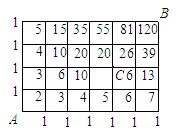
【解析】本題是最短路線問題.要找出共有多少種不同走法,關鍵是保證不重也不漏,一般采用標數法.如上圖所示,共有120種.
另解:本題也可采用排除法.由于不能經過C,可以先計算出從A到B的最短路線有多少條,再去掉其中那些經過C的路線數,即得到所求的結果.
對于從A到B的每一條最短路線,需要向右6次,向上4次,共有10次向右或向上;而對于每一條最短路線,如果確定了其中的某6次是向右的,那么剩下的4次只能是向上的,從而該路線也就確定了.這就說明從A到B的最短路線的條數等于從10次向右或向上里面選擇6次向右的種數,為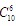 .
.
一般地,對于m*n的方格網,相對的兩個頂點之間的最短路線有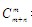 種.
種.
本題中,從A到B的最短路線共有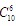 種;從A到C的最短路線共有
種;從A到C的最短路線共有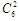 種,從C到B的最短路線共有
種,從C到B的最短路線共有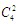 種,根據乘法原理,從A到B且必須經過C的最短路線有
種,根據乘法原理,從A到B且必須經過C的最短路線有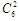 *
*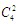 種,所以,從A到B且不經過C的最短路線有
種,所以,從A到B且不經過C的最短路線有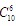 -
-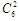 *
*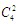 =210-90=120種.
=210-90=120種.
 編輯推薦:
編輯推薦:
-------------------------------------------------------------------------------------
《小學奧數系統總復習》 圖書簡介
 |
《小學奧數系統總復習》分 上下兩冊,涵蓋了奧數中8大專題,共設21講。每講設置4大模塊,即闖關目標、賽前熱身、實戰演練和逐級闖關,構建了完整的奧數知識體系,全面覆蓋小學奧 數知識。此外,本書對部分經典例題錄制了視頻,免費贈送給各位學員。本書附有2010年和2011年的北京集訓隊選拔試題,為本書增加了新的亮點。 為了讓大家更好的獲得知識、理解知識,本書設有論壇交流環節,讀者可以登錄E度論壇點擊進入圖書答疑帖,即可實現在線提問、交流心得,名師天天坐鎮論壇,等你來交流! |



