學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽 中奪取佳績的學生。
·本周試題由學而思奧數名師鐘森精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
難度:★★★★
小學六年級奧數天天練:構造與論證
有3堆小石子,每次允許進行如下操作:從每堆中取走同樣數目的小石子,或是將其中的某一石子數是偶數的堆中的一半石子移入另外的一堆.開始時,第一堆有1989塊石子,第二堆有989塊石子,第三堆有89塊石子.問能否做到:
(1)某2堆石子全部取光?
(2)3堆中的所有石子都被取走?
【答案】
(1)可以,如(1989,989,89) (1900,900,0) (950,900,950)
(50,0,50) (25,25,50) (O,0,25).
(2)因為操作就兩種,每堆取走同樣數目的小石子,將有偶數堆石子堆中一半移至另一堆,所以每次操作石子總數要么減少3的倍數,要么不變.
現在共有1989+989+89=3067,不是3的倍數,所以不能將3堆中所有石子都取走.
難度:★★★★★
小學六年級奧數天天練:構造與論證
如圖,將1,2,3,4,5,6,7,8,9,10這10個數分別填入圖中的10個圓圈內,使任意連續相鄰的5個圓圈內的各數之和均不大于某個整數M.求M的最小值并完成你的填圖.
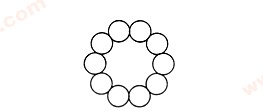
【答案】
要使M最小,就要盡量平均的填寫,因為如果有的連續5個圓圈內的數特別小,有的特別大,那么M就只能大于等于特別大的數,不能達到盡量小的目的.
因為每個圓圈內的數都用了5次,所以10次的和為5×(1+2+3+…+10)=275.
每次和都小于等于朋,所以IOM大于等于275,整數M大于28.
下面來驗證M=28時是否成立,注意到圓圈內全部數的總和是55,所以肯定是一邊五個的和是28,一邊是27.因為數字都不一樣,所以和28肯定是相間排列,和27也是相問排列,也就是說數組每隔4個差值為l,這樣從1填起,容易排出適當的填圖.




