日常生活中的數學----打電話
來源:網絡 2008-02-21 09:25:28

每次當你拿起電話聽筒打電話,發傳真,或發調制解調器信息時,你就進入了非常復雜的巨大網絡。覆蓋全球的通信網是驚人的。很難想像每天有多少次電話在這網絡上打來打去。一個系統被不同國家和水域的不同系統“分割”,它是如何運行的呢?一次電話是如何通向在你的城市、你的國家或另一國家中的某個人的呢?
在早期電話史上,打電話的人拿起電話聽筒,搖動曲柄,與接線員聯系。一位本地接線員的聲音從本地交換臺來到線上,說“請報號碼”,然后他把你同你試圖通話的對方連接起來。如今,這一過程由于有了各種不同的轉換和送達通話的方法而如雨后春筍般地迅速發展。包含著線性規劃的各種復雜類型,以及有關的二進制和二進編碼的數學,已脫離了潛在的不穩固地位而成為有意義的東西。
你的聲音是如何行進的?你的聲音產生聲波,在聽筒中轉換成電信號。今天,這些電脈沖可以用許多不同的方法傳遞和轉換。它們可以變成激光信號,然后沿光纖電纜傳遞①;它們可以轉換成無線電信號,然后利用無線電或微波線路在一個國家內從一座塔傳送到另一座塔;或者它們可以仍舊作為電信號沿著電話線傳送。在美國,大部分電話都是由自動交換系統接通的。現在電子交換系統是最快的。這系統有一個程序,這程序包含電話運行的所有方面所需的信息,并且時刻在了解哪些電話正在使用,哪些通道是可用的。通話可以由不同頻率的電流傳送,或轉換成數字信號。這兩種方法都使多重通話可以沿同一些電線傳送。最新式的系統把通話轉換成數字信號,然后再用二進制數列編碼。于是各個通話可以沿著線路以特定的次序“同時”行進,直到它們被譯碼而到達各自的目的地。
1947年,數學家喬治B.丹齊克研究出了求解復雜線性規劃問題的單純形法。單純形法實質上是沿著那立體的棱進行,依次檢查每一隅角,并總是向著最優解前進。當可能解的數目不超過15000~20000時,這方法能有效地求得解答。1984年,數學家納倫德拉·卡馬卡發現一種方法,它使求解很麻煩的線性規劃問題例如長距離電話最優通話線路問題所需的時間大為縮短。卡馬卡算法采取了一條通過那立體內部的捷徑。在選擇了一個任意內點之后,這算法使整個結構變形,以把問題改造得使所選擇的點正好在那立體的中心。下一步是朝著最優解的方向找到一個新的點,再將結構變形,又使新點位于中心。必須進行變形,否則那些看來能給出最優改進的方向都是虛假的。這些重復的變換以射影幾何的概念為基礎,很快便能得到最優解。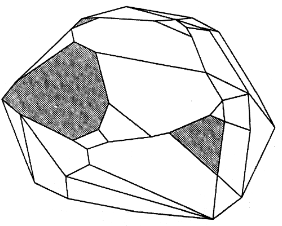
打電話時,電話系統選擇最佳通話途徑,并發出一連串指令,以接通線路。整個過程只需幾分之一秒。通話線路最好是直接通向對方的——從節省距離和時間的觀點看來,這是人們所期望的。但是如果直接線路正在為別的通話服務,新的通話就必須沿其他線路中最好的一條進行。這正是需要用到線性規劃②的地方。我們把電話線路問題當作一個有幾百萬個面的復雜幾何立體形來看。每個頂點代表一個可能的解。問題是要找出最優解,而不必計算每一個解。
今天,古老的電話敬語“請報號碼”具有雙重的意義。曾經是簡單的拿起電話聽筒打電話的過程,現在卻要使一個依靠著數學的龐大而復雜的網絡運作起來。
①“同時”通話數可從96到13000以上,這視所用線路類型而定。光纖系統能比傳統的銅/鋁纜運載更多的信息。
②線性規劃技術可用來解決許多不同的問題。這些問題通常有許多條件和變量。可以用一個農業問題作簡單例子:一個農民要想決定如何最有效地利用他(她)的土地使產量和收益達到最大。條件和變量包括諸如這些事情:考慮不同的作物,每種作物需要多少土地,每種作物單產多少,每種作物售出后獲得多少收入。為解這樣一個問題,人們就每一條件寫出線性不等式和/或方程,并在二維坐標圖中一個多邊形區域上求解。
相關文章
- 小學1-6年級作文素材大全
- 全國小學升初中語數英三科試題匯總
- 小學1-6年級數學天天練
- 小學1-6年級奧數類型例題講解整理匯總
- 小學1-6年級奧數練習題整理匯總
- 小學1-6年級奧數知識點匯總
- 小學1-6年級語數英教案匯總
- 小學語數英試題資料大全
- 小學1-6年級語數英期末試題整理匯總
- 小學1-6年級語數英期中試題整理匯總
- 小學1-6年語數英單元試題整理匯總