【答案】
分析:由題意可知,正方形的邊長即是2703和1113的最大公約數。在學校,我們已經學過用短除法求兩個數的最大公約數,但有時會遇到類似此題情況,兩個數除了1以外的公約數一下不好找到。但又不能輕易斷定它們是互質數。怎么辦?在此,我們以此題為例介紹另一種求最大公約數的方法。
可做如下圖解:
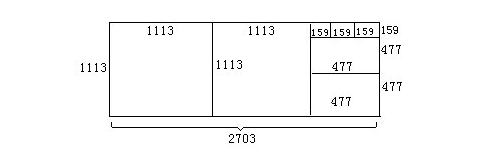
從圖中可知:在長2703厘米、寬1113厘米的長方形紙的一端,依次裁去以寬(1113厘米)為邊長的正方形2個.在裁后剩下的長1113厘米,寬477厘米的長方形中,再裁去以寬(477厘米)為邊長的正方形2個.然后又在裁剩下的長方形(長477厘米,寬159厘米)中,以159厘米為邊長裁正方形,恰好裁成3個,且無剩余.因此可知,159厘米是477厘米、1113厘米和2703厘米的約數.所以裁成同樣大的,且邊長盡可能長的正方形的邊長應是159厘米.所以,159厘米是2703和1113的最大公約數。
讓我們把圖解過程轉化為計算過程,即:
2703÷1113,商2余477;
1113÷477,商2余159;
477÷159,商3余0。
或者寫為
2703=2×1113+477,
1113=2×477+159,
477=3×159。
當余數為0時,最后一個算式中的除數159就是原來兩個數2703和1113的最大公約數.
可見,477=159×3,
1113=159×3×2+159=159×7,
2703=159×7×2+477
=159×7×2+159×3=159×17。
又∵7和17是互質數,
∴159是2703和1113的最大公約數。
我們把這種求最大公約數的方法叫做輾轉相除法.輾轉相除法的優點在于它能在較短的時間內求出任意兩個數的最大公約數。



