奧數題及答案:
學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中奪取佳績的學生。
·本周試題由學而思奧數名師精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
【計算】
1、難度:★★★★
下面方陣中所有數的和是多少?
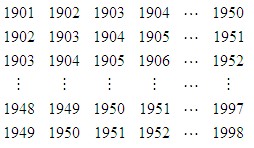
【分析】我們不難看出,每一行、每一列都是一個等差數列,通過觀察,每一列的相鄰兩個數都相差1,由于每一行都有50個數字,所以每行的和構成公差為50的等差數列.
第一行的和我們可以求出,為:(1901+1950)×50÷2=96275
一共有(1949-1901+1)行,每行的和構成首項為96275,公差為50,項數為49的等差數列,那么最后一行的和為:96275+50×(49-1)=98675,所以,方陣中所有數的總和為
(96275+98675)×49÷2=4776275 .
[鞏固]把自然數按下面形式排列,它的第一行是1、2、4、7、11……那么第一行的第100個數是幾?
1,2,4,7,1l,……
3,5,8,12,……
6,9,13, ……
10,14,……
15, ……
……
分析:觀察上面數的排列規律,從左上方到右下方看斜行,依次是1,(2,3),(4,5,6),(7,8,9,10),……各斜行數的個數順次是1,2,3,4,……所以第一行的第100個數,正好是第100個斜行的第一個數.(1+2+3+……+98+99)+1 =(1+99)×99÷2+1=4951 .
2、難度:★★★★★
用3根等長的火柴棍擺成一個等邊三角形,用這樣的等邊三角形,按圖所示鋪滿一個大的等邊三角形,如果這個大的等邊三角形的底邊放10根火柴,那么一共要放多少根火柴?
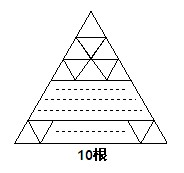
【分析】如果把圖中最上端的一個三角形看作第一層,與第一層緊相連的三個三角形(向上的三角形2個,向下的三角形1個)看作第二層,那么這個圖中一共有10層三角形.
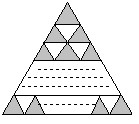
這10層三角形每層所需火柴數就是構成上圖中所有陰影三角形的邊數和.自上而下依次為:3,6,9,……,3×10.
它們成等差數列,而且首項為3,公差為3,項數為10.
求火柴的總根數,就是求這個等差數列各項的和,即
3+6+9+……+30=(3+30)×10÷2=33×5=165(根)
所以,一共要放165根火柴.



