奧數題及答案:
學而思奧數天天練欄目每日精選中等、高等難度試題各一道。中難度試題適合一些有過思維基礎訓練、考題學習經歷,并且奧數成績中上的學生。高難度試題立足于杯賽真題、綜合應用和加深各知識點,適合一些志在競賽中奪取佳績的學生。
·本周試題由學而思奧數名師精選、解析,以保證試題質量。
·每周末,我們將一周試題匯總為word版本試卷,您可下載打印或在線閱讀。
·每道題的答題時間不應超過15分鐘。答案明日公布!
1.難度:★★★★
(新加坡小學數學奧林匹克競賽)下圖是一個方格網,計算陰影部分的面積.
【分析】擴展法。把所求三角形擴展成正方形ABCD中.這個正方形中有四個三角形:一個是要求的△AEF;另外三個分別是:△ABE、△FEC、△DAF,它們都有一條邊是水平放置的,易求它們的面積分別為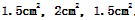 .所以,圖中陰影部分的面積為:3×3-(1.5×2+2)=4(
.所以,圖中陰影部分的面積為:3×3-(1.5×2+2)=4(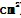 ).
).
2.難度:★★★★
如圖(a),有21個點,每相鄰三個點成"∵"或"∴",所形成的三角形都是等邊三角形.計算三角形ABC的面積.
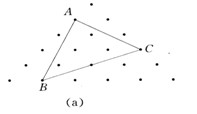
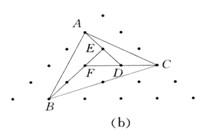
【分析】(法1)如圖(b)所示,在△ABC內連接相鄰的三個點成△DEF,再連接DC、EA、FB后是△ABC可看成是由△DEF分別延長FD、DE、EF邊一倍、一倍、二倍而成的,由等積變換不難得到S△ACD=2, S△AEB=3, S△FBC=4,所以S△=1+2+3+4=10(面積單位).
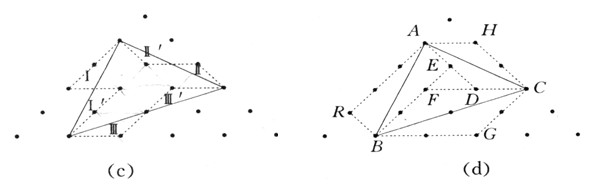
(法2)如圖(c)所示,作輔助線把圖Ⅰ′、Ⅱ′、Ⅲ′分別移拼到Ⅰ、Ⅱ、Ⅲ的位置,這樣可以通過數小正三角形的方法,求出△ABC的面積為10.
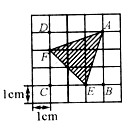
(法3)如圖(d)所示:作輔助線可知:平行四邊形ARBE中有6個小正三角形,而△ABE的面積是平行四邊形ARBE面積的一半,即S△ABE=3,平行四邊形ADCH中有4個小正三角形,而△ADC的面積是平行四邊形ADCH面積的一半,即S△ADC=2.平行四邊形FBGC中有8個小正三角形,而△FBC的面積是平行四邊形FBGC的一半,即:S△FBC=4. 所以三角形ABC的面積是1+2+3+4=10(面積單位).