奧數 > 小學試題庫 > 單元測試 > 數學單元測試 > 六年級數學單元測試上冊 > 正文
2011-11-18 15:09:59

小學數學總復習專題講解及訓練(八)
主要內容
解決問題的策略
學習目標
1、讓學生在直觀的情境中想到轉化,并應用圖形的平移和旋轉知識進行圖形的等積,等周長的變形。
2、在解決實際問題過程中體會轉化的含義和應用的手段,感受轉化在解決這個問題時的價值。
3、進一步積累解決問題的經驗,增強解決問題的“轉化”意識,提高學好數學的信心。
考點分析
轉化能把新穎的問題變成已經認識、已能解決的問題,從而創造性地利用已有的知識,經驗。
典型例題
例1、(運用轉化的策略巧算周長)求下面圖形的周長。(單位:厘米)
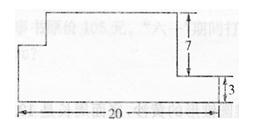
分析與解:求這個圖形的周長,就是求圍成這個圖形的所有線段的長度和。圖中有的線段的長度不知道,可以將其中的4條線段進行平移(如下圖),平移之后形成一個長方形,長方形的周長和原來圖形的周長是相等的。因此求原來圖形周長的問題就轉化成了求下圖這個長方形的周長。
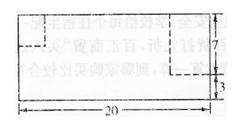
解答:(20 + 7 +3)× 2 = 60(厘米)
點評:通過相等面積的代換轉化,把一些不規則的圖形轉化為規則的、容易判斷的圖形,這就是轉化的優點,在解答時要靈活運用。
例2、(將復雜的圖形轉化成簡單的圖形后計算面積)
如圖1是一塊長方形草地,長方形的長是16米,寬是10米。中間有兩條道路,一條是長方形,一條是平行四邊形。草地部分的面積有多大?
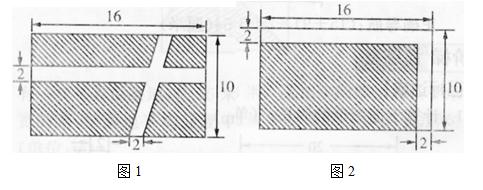
分析與解:求草地部分的面積,可以用大長方形的面積減去兩條道路的面積,但要考慮兩條道路的重疊部分,因此計算比較復雜。可以將圖1轉化成圖2,兩條道路轉化到了長方形草地的邊上,很明顯,圖2草地部分(陰影部分)的面積和圖1相等,現在求草地的面積轉化成了求長方形的面積,計算比較簡單。
解答:(16 - 2 )× (10 - 2) = 112(平方米)
答:草地部分的面積是112平方米。
例3、(辨析)下面圖形的周長可以轉化成長15厘米、寬9厘米的長方形來計算,即周長是(15 + 9)× 2 = 48(厘米)。
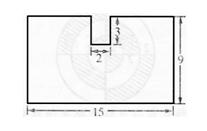
分析與解:如下圖,將長2厘米的線段移到上面,轉化成了一個長方形,但還多兩條3厘米的線段。
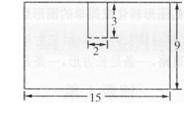
正確解答:(15 + 9)× 2 + 3 × 2 = 54(厘米)

歡迎掃描二維碼
關注奧數網微信
ID:aoshu_2003

歡迎掃描二維碼
關注中考網微信
ID:zhongkao_com