車過橋問題是行程問題的一種,也有路程、速度與時(shí)間之間的數(shù)量關(guān)系,同時(shí)還涉及車長、橋長等問題。基本數(shù)量關(guān)系是火車速度×時(shí)間=車長+橋長
【例題解析】
例1 一列火車長150米,每秒鐘行19米。全車通過長800米的大橋,需要多少時(shí)間?
分析 列車過橋,就是從車頭上橋到車尾離橋止。車尾經(jīng)過的距離=車長+橋長,車尾行駛這段路程所用的時(shí)間用車長與橋長和除以車速。
解:(800+150)÷19=50(秒)
答:全車通過長800米的大橋,需要50秒。
【邊學(xué)邊練】
一列火車長200米,它以每秒10米的速度穿過200米長的隧道,從車頭進(jìn)入隧道到車尾離開隧道共需要多少秒?
例2 一列火車長200米,以每秒8米的速度通過一條隧道,從車頭進(jìn)洞到車尾離洞,一共用了40秒。這條隧道長多少米?
分析 先求出車長與隧道長的和,然后求出隧道長。火車從車頭進(jìn)洞到車尾離洞,共走車長+隧道長。這段路程是以每秒8米的速度行了40秒。
解:(1)火車40秒所行路程:8×40=320(米)
(2)隧道長度:320-200=120(米)
答:這條隧道長120米。
【邊學(xué)邊練】
一支隊(duì)伍1200米長,以每分鐘80米的速度行進(jìn)。隊(duì)伍前面的聯(lián)絡(luò)員用6分鐘的時(shí)間跑到隊(duì)伍末尾傳達(dá)命令。問聯(lián)絡(luò)員每分鐘行多少米?
例3 一列火車長119米,它以每秒15米的速度行駛,小華以每秒2米的速度從對(duì)面走來,經(jīng)過幾秒鐘后火車從小華身邊通過?
分析 本題是求火車車頭與小華相遇時(shí)到車尾與小華相遇時(shí)經(jīng)過的時(shí)間。依題意,必須要知道火車車頭與小華相遇時(shí),車尾與小華的距離、火車與小華的速度和。
解:(1)火車與小華的速度和:15+2=17(米/秒)
(2)相距距離就是一個(gè)火車車長:119米
(3)經(jīng)過時(shí)間:119÷17=7(秒)
答:經(jīng)過7秒鐘后火車從小華身邊通過。
【邊學(xué)邊練】
一人以每分鐘60米的速度沿鐵路步行,一列長144米的客車對(duì)面開來,從他身邊通過用了8秒鐘,列車的速度是每秒多少米?
例4 一列火車通過530米的橋需40秒鐘,以同樣的速度穿過380米的山洞需30秒鐘。求這列火車的速度是每秒多少米?車長多少米?
分析與解 火車40秒行駛的路程=橋長+車長;火車30秒行駛的路程=山洞長+車長。比較上面兩種情況,由于車長與車速都不變,所以可以得出火車40-30=10秒能行駛530-380=150米,由此可以求出火車的速度,車長也好求了。
解:(1)火車速度:(530-380)÷(40-30)=150÷10=15(米/秒)
(2)火車長度: 15×40-530=70(米)
答:這列火車的速度是每秒15米,車長70米。
【邊學(xué)邊練】
一列火車通過440米的橋需要40秒,以同樣的速度穿過310米的隧道需要30秒.這列火車的速度和車身長各是多少?
例5 某人沿著鐵路邊的便道步行,一列客車從身后開來,在身旁通過的時(shí)間是15秒鐘,客車長105米,每小時(shí)速度為28.8千米.求步行人每小時(shí)行多少千米?
分析 一列客車從身后開來,在身旁通過的時(shí)間是15秒鐘,實(shí)際上就是指車尾用15秒鐘追上了原來與某人105米的差距(即車長),因?yàn)檐囬L是105米,追及時(shí)間為15秒,由此可以求出車與人速度差,進(jìn)而求再求人的速度。
解:(1)車與人的速度差:105÷15=7(米/秒)=25.2(千米/小時(shí))
(2)步行人的速度:28.8-25.2=3.6(千米/小時(shí))
答:步行人每小時(shí)行3.6千米。
【邊學(xué)邊練】
一人以每分鐘60米的速度沿鐵路邊步行,一列長144米的客車從他身后開來,從他身邊通過用了8秒鐘,求列車的速度。
例6:兩人沿著鐵路線邊的小道,從兩地出發(fā),兩人都以每秒1米的速度相對(duì)而行。一列火車開來,全列車從甲身邊開過用了10秒。3分后,乙遇到火車,全列火車從乙身邊開過只用了9秒。火車離開乙多少時(shí)間后兩人相遇?
分析 根據(jù)題意圖示如下:
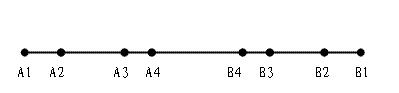
火車過橋問題
A1、B1 分別表示車追上甲時(shí)兩人所在地點(diǎn), A2、B2 分別為車從甲身邊過時(shí)兩人所在地點(diǎn), A3、B3 分別為車與乙相遇時(shí)兩人所在地點(diǎn),A4、B4分別為車從乙身邊開過時(shí)兩人所在地點(diǎn)。要求車從乙身邊開過后甲乙相遇時(shí)間用A4到B4之間的路程除以兩人速度和。
解:(1)求車速
(車速-1)×10=10×車速-10=車長
(車速+1)×9 = 9×車速+ 9=車長
比較上面兩式可知車速是每秒19米。
(2)A3到B3的路程,即車遇到乙時(shí)車與甲的路程差,也是甲與乙的相距距離。
(19-1)×(10+190)=3420(米)
(3)A4到B4的路程,即車從乙身邊過時(shí)甲乙之間的路程。
3420-(1+1)×9=3402(米)
(4)車離開乙后,甲乙兩人相遇的時(shí)間為
3402÷(1+1)=1701(秒)
答:火車離開乙1701秒后兩人相遇
【邊學(xué)邊練】
甲、乙二人沿鐵路相向而行,速度相同,一列火車從甲身邊開過用了8秒鐘,離甲后5分鐘又遇乙,從乙身邊開過,只用了7秒鐘,問從乙與火車相遇開始再過幾分鐘甲乙二人相遇? (提示:設(shè)步行速度為每秒1米)



