例3 數一數,圖3-9中共有多少個銳角?
解:(1)我們知道,圖中任意兩條從O點發出的射線都組成一個銳角.
所以,以OA邊為公共邊的銳角有:
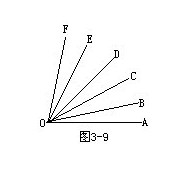
∠LAOB,∠AOC,∠AOD,∠AOE,
∠AOF共5個.
以OB邊為公共邊的銳角有:∠BOC,∠BOD,∠BOE,∠BOF共4個.
以OC邊為公共邊的銳角有:∠COD,∠COE,∠COF共3個.以OD邊為公共邊的銳角有:∠DOE,∠DOF共2個.以OE邊為一邊的銳角有:∠EOF只1個.
銳角總數5+4+3+2+1=15(個).
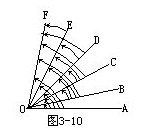
②用圖示法更為直觀明了:如圖3-10所示,銳角總數為:5+4+3+2+1=15(個).
想一想:①由例3可知:由一點發出的六條射線,組成的銳角的總數=5+4+3+2+1(個),由此猜想出如下規律:(見圖3-11~15)
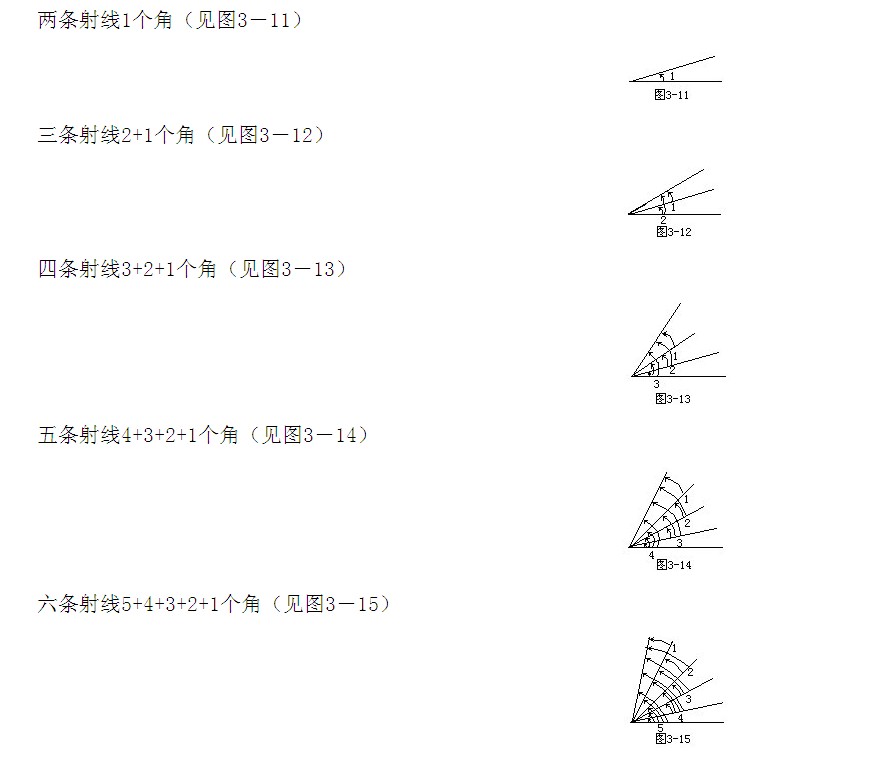
總之,角的總數是從1開始的一串連續自然數之和,其中最大的自然數比射線數小1.
②同樣,也可以這樣想:如果把相鄰兩條射線構成的角叫做基本角,那么有共同頂點的基本角和角的總數之間的關系是:
角的總數是從1開始的一串連續自然數之和,其中最大的自然數等于基本角個數.
③注意,例2和例3的情況極其相似.雖然例2是關于線段的,例3是關于角的,但求總數時,它們有同樣的數學表達式.同學們可以看出,一個數學式子可以表達表面上完全不同的事物中的數量關系,這就是數學的魔力.



