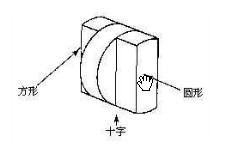
21.方形、十字與圓形
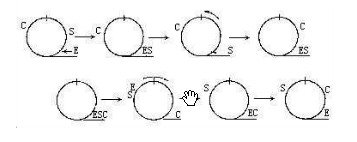
22.火車司機的困擾
這個問題與第33題相當類似.關鍵是把C轉至主線上,如圖所示.
23.聰明的牛奶商
先把3升的瓶子裝滿,然后把瓶子中的牛奶倒入5升的瓶子;再把3升的瓶子裝滿,然后把瓶中的牛奶倒入5升的瓶子,直到裝滿為止.這時留在3升的瓶子內的牛奶正好是1升.用這種量出1升牛奶的方法,理論上可以量出任何升數為整數的牛奶.不過,顯然這并不是最有效率的方法.5升與3升可以直接量出,其他如6=3+3,8=5+3,所以要量出6升與8升很容易.但要如何量出7升與4升呢?
24.士兵的遭遇
這題與第12題與第35題類似,這種問題早在本世紀初期就相當流行了.這個問題的關鍵是獨木舟能載兩個小孩,但只需要一個小孩就能劃獨木舟過河.一個小孩先劃獨木舟至左岸,然后一個士兵帶著槍與裝備劃到右岸.
第二個小孩再把船劃到左岸,把第一個小孩接回到右岸.重復此程序,直到每一位士兵都過河為止.
25.等寬曲線
石塊向前移動2m.
雖然有許多形狀都可作為滾輪的橫切面,但只有圓形可作為輪子——除非你想有段顛簸的旅程!要作最平滑的移動,輪軸必須位于輪子的中心.當然,也只有圓形的輪子,車軸至輪緣的距離都相等.
26.莫比烏斯帶
過去沒有接觸過莫比烏斯帶的人,對于這個活動的結果通常會感到非常驚訝.運用系統化的方法,可以找到紙帶扭轉次數與從中間剪開后的結果之間的關系.
這個活動非常好玩,但除了好玩之外,它同樣具有值得探討的意義.
27.內還是外
A與B在內部,C在外部.
每跨越圍墻一次,不是由內至外,就是由外至內.
任何繞著環建成的圓形監獄,或是如同赤道一樣的監獄,無內外之分.
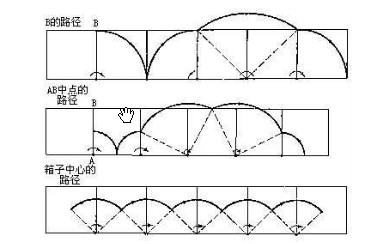
28.滾箱子
只要包裝箱是繞邊緣旋轉,所有路徑都是呈圓弧形.
29.輪子往何處去
把A、B、C、D與輪子滾動瞬間的軸連線(圖中的虛線),則,A、B、C、D的運動方向就是與所連直線垂直的箭頭方向.
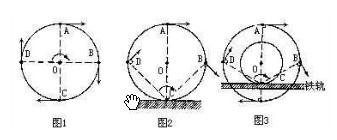
圖1中的輪子繞中心O旋轉.
圖2中的輪子繞C點旋轉,C點是與地面接觸的點.
圖3中的輪子繞與鐵軌接觸的點旋轉.
在每一種情況中,A都是由左向右移動,但B與D的移動方向變化就相當大.由圖3還可以看出火車往前走得愈快,C點向后移動的速度也會愈快.
30.齒輪系統
(1)逆時針方向,4圈.
(2)順時針方向,1圈.
(3)逆時針方向,1圈.
(4)順時針方向,1/2圈.
規則1:輪軸的數目為偶數時,通常最后一個輪軸與第一個輪軸的旋轉方向相反.
規則2:在一個輪軸上如果只有一個齒輪,如圖中(1)、(2)、(3)、(4)的情形,B的旋轉圈數只與A和B的齒數有關:
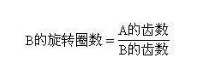
在圖中(5)、(6)、(7)的情形中,需要把齒輪系統分解成數個部分,則上述規則方能適用.
(5)A每轉1圈,第二個輪軸要轉3圈.第二個輪軸每轉1圈,B要轉4圈.所以A轉1圈,會使B轉12圈(3×4).由于輪軸數為奇數,B的旋轉方向與A相同.
(6)A每轉1圈,第二個輪軸要轉1/3圈.第二個輪軸轉1圈,會使第三個輪軸轉2/3圈.第三個輪軸轉1圈,會使B轉1/2圈.所以只要A每轉1圈,會使B轉1/3×2/3×1/2=1/9圈.由于輪軸數為偶數,B的旋轉方向與A相反.
(7)A轉1圈,第二個輪軸要轉3圈.第二個輪軸轉1圈,B要轉1.5圈.所以A轉一圈,會使B轉4.5圈(3×1.5).由于輪軸數為奇數,所以B的旋轉方向與A相同.
下圖是將60齒、36齒、12齒及24齒的齒輪設計成的齒輪系統.
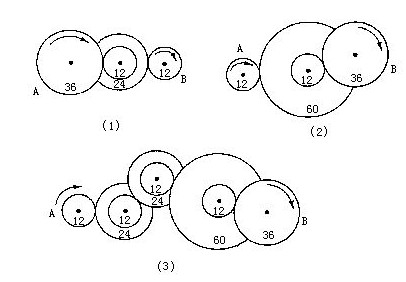
有時可利用齒輪系統增加旋轉速度,如手動的鉆子或打蛋器;有時也可用來減速,如時鐘、食物攪拌器或唱盤等等.
要改變輸出輪軸的運動方向,可以在齒輪系統中再加一個只有單一齒輪的輪軸.這個多加的齒輪的齒數,并不會改變齒輪系統整體的轉速大小.



